The philosophy that led to the formula
Bodies on the Earth tend to go down. Meaning they experience a force pulling them towards the ground. We know this because when simply leaving an object in the air we see that it accelerates towards the ground. Due to Newton’s second law of motion we know this means there is a force acting on it in that direction.
But what direction is “the ground”?
It is known at least since the ancient greeks that the earth is round. Therefore, in order to solve this riddle people said that instead of falling towards “the ground”, objects fall towards the “center of the earth”.
OK, so we know the direction of gravity, but what is its strength?
Galileo demonstrated in a famous experiment that an object’s mass doesn’t change it’s acceleration due to gravity. This constant acceleration was measured to be around g\approx 9.8_{\frac{m}{s^2}}. So an object falling on the earth would increase its speed by 9.8 meters per second in each second.
Due to the second law of motion we know that a=\frac{F}{m} so the force of gravity on earth acting on an object with mass m is F_G\approx mg.
The next question that brought a breakthrough was: what do we mean “on earth”?
As the image above suggests, is the moon also an object “on earth” that is just very far away? Or is it something else? When does an object stop being on earth?
Newton pondered this question for a while and his answer was: every object is on earth! Some objects are just very far away, but they still feel earth’s gravitational pull. Well… then why doesn’t the Moon fall towards the earth like the apple? Here was Newton’s genius, he proposed, the earth does fall towards the earth like the apple, but it also moves sideways very very quickly.
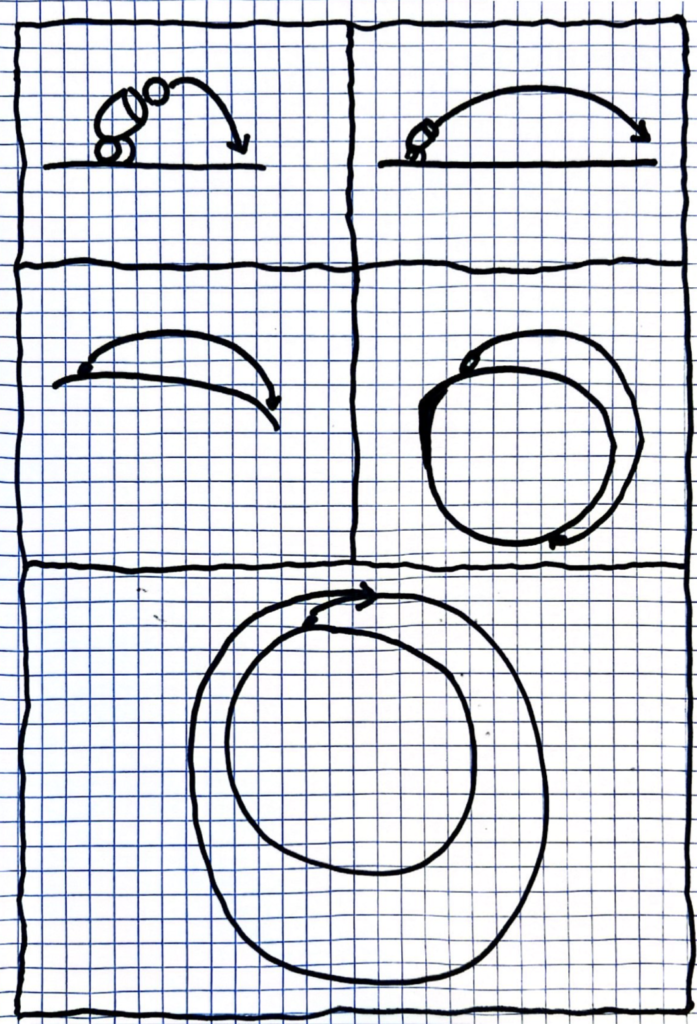
Because the Moon moves sideways so quickly, the ground falls away from it at the same rate at which the Moon falls towards the ground. So the Moon never reaches the ground at all! It just goes around the Earth in circles – called orbits.
The next extraordinary question was, why does the apple fall towards the Earth but not towards the Moon?
The obvious answer might be, the Earth is closer. But Newton just proposed that everything is “on Earth” (just far away), so everything must also be “on the Moon” and feel its gravitational pull as well.
Newton’s solution was proposing that the gravitational force that an object exerts is inversely proportional to the distance from that object, F_G\propto \frac{1}{r^k}. As long as the distance is greater, the force will be smaller.
OK, but if we hold two apples close together they still don’t fall towards each other. So why does an apple fall towards the Earth or feels the gravitational pull of the Moon, but not of the other apple?
For this, Newton also had a miraculous answer, the apple does feel the other apples gravitational pull, it is just very small because the apples are not massive. So he concluded: the gravitational pull an object with mass m feels from an object of mass M is proportional to m^nM^n for some constant n. So now Newton had the formula:
F_G\propto \frac{m^nM^n}{r^k}
Another stroke of genius by Newton was discovering that n=1 and k=2 (how he did that is explained in the appendix). Meaning that
F_G\propto \frac{mM}{r^2}
After some time, Henry Cavendish did an experiment to find the proportionality constant and he found that
F_G\propto \frac{GmM}{r^2}
Where G\approx 6.67\cdot 10^{-11}_{\frac{m^3}{kg\cdot s^2}}.
And this is Newton’s law of gravitation!
The force of gravitation between two bodies of mass m_1 and m_2 that are at a distance r from one another is
F=\frac{Gm_1m_2}{r^2}
This equation is revolutionary. It helps us deduce the behaviors of any body that has mass due to the force of gravity. For example, it helped physicists deduce that the orbits of planets around their stars are always ellipses. They also tell that if an object (e.g. asteroid) goes through the solar system but doesn’t enter an orbit, then its path through the solar system must be a hyperbola or a parabola.
This equation is really useful. Scientists use it to predict if certain asteroids are dangerous to Earth. It was used to conduct the lunar landing and is still used when launching satellites into orbit.
One simple use of the equation is to calculate the mass of the Earth.
Calculating mass of the Earth
If we look at an object of mass m slightly above the surface of the Earth. We let it fall and it accelerates at g. But we know the acceleration is also \frac{F}{m}=\frac{GM_\oplus}{R_\oplus^2}. Where M_\oplus is the mass of the Earth and R_\oplus is its radius. This is because the object is falling due to the gravity of the Earth and its distance from the center of the Earth is approximately its radius. So
g=\frac{GM_\oplus}{R_\oplus^2}
Rearranging we get
M_\oplus = \frac{gR_\oplus^2}{G}
The value of R_\oplus was known to be about 6366\cdot 10^3_m from the time of the greeks. So if we use our known values we get
M_\oplus \approx \frac{9.8\cdot (6366 * 10^3)^2}{6.67*10^{-11}}=5.95\cdot10^{24}_{kg}
This is quite a lot! The Earth is heavy 🙂
Appendix
How did Newton deduce from
F_G\propto \frac{m^nM^n}{r^k}
That n=1 and k=2?
The part of n=1 is pretty easy. It was known that a body on the earth experiences F\propto mg as we saw before. So from this we get n=1.
What about k=2? Lets assume that an object is at an orbit around the earth due to gravity. It is known that for a circular orbit the acceleration is
a=\frac{4\pi^2 r}{T^2}
Where r is the radius of the orbit and T is the time it takes to complete it.
Kepler’s third law – which was known in Newtons time claims that for any circular orbit due to gravity:
T^2\propto r^3
So we get that a\propto \frac{1}{r^2} and hence k=2.
*Kepler’s laws were found empirically based on long and tedious observations by astronomer Tycho Brahe

